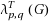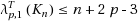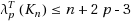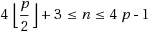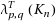(p,q)‐total labeling of complete graphs

Given a graph G and positive integers p,q with p≥q, the (p,q)‐total number 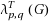${\lambda }_{p,q}^T(G)$ of G is the width of the smallest range of integers that suffices to label the vertices and the edges of G such that the labels of any two adjacent vertices are at least q apart, the labels of any two adjacent edges are at least q apart, and the difference between the labels of a vertex and its incident edges is at least p. Havet and Yu (2008) first introduced this problem and determined the exact value of ${\lambda }_{p\mathrm{,1}}^T(K_n)$ except for even n with p+5≤n≤6p ²−10p+4. 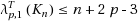Their proof for showing that ${\lambda }_{p\mathrm{,1}}^T(K_n)\le n+2p‐3$ for odd n has some mistakes. In this paper, we prove that if n is odd, then 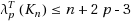${\lambda }_p^T(K_n)\le n+2p‐3$ if p=2, p=3, or 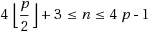$4\lfloor \frac{p}{2}\rfloor +3\le n\le 4p-1$ . And we extend some results that were given in Havet and Yu (Discrete Math 308:496–513, 2008). Beside these, we give a lower bound for 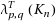${\lambda }_{p,q}^T(K_n)$ under the condition that q <p <2q.