The decycling number of outerplanar graphs

For a graph G, let τ(G) be the decycling number of G and c(G) be the number of vertex‐disjoint cycles of G. It has been proved that c(G)≤τ(G)≤2c(G) for an outerplanar graph G. An outerplanar graph G is called lower‐extremal if τ(G)=c(G) and upper‐extremal if τ(G)=2c(G). In this paper, we provide a necessary and sufficient condition for an outerplanar graph being upper‐extremal. 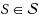On the other hand, we find a class $𝒮$ of outerplanar graphs none of which is lower‐extremal and show that if G has no subdivision of S for all $S\in 𝒮$ , then G is lower‐extremal.