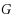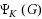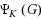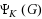| Article ID: | iaor20132658 |
| Volume: | 21 |
| Issue: | 1 |
| Start Page Number: | 13 |
| End Page Number: | 25 |
| Publication Date: | Jun 2013 |
| Journal: | Central European Journal of Operations Research |
| Authors: | Gvozdenovi Neboja, Povh Janez, Govorin Jelena |
| Keywords: | heuristics |
The Lovász theta number Lovász (1979) is a well‐known lower bound on the chromatic number of a graph