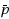We consider an M/G/1 retrial queue with negative customers and priority under Bernoulli vacation schedule subject to the server breakdowns and repairs. Arrivals of both positive customers and negative customers are two independent Poisson processes. Positive customers receive service immediately if the server is idle upon their arrivals. Otherwise, they may either with probability p join the priority queue or with complementary probability
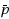enter a retrial orbit. A breakdown at the busy server is represented by the arrival of a negative customer which causes the the customer being in service to be lost. The server takes Bernoulli vacation after a service or a repair completion. It is assumed that the server has arbitrary repair time and vacation time distributions. With the help of Lyapunov functions we have obtained the necessary and sufficient condition for ergodicity of embedded Markov chain. By applying the supplementary variables method, we obtain the steady‐state solutions for both queueing measures and reliability quantities. Moreover, we investigate the stochastic decomposition law. Besides, some special cases of interest are discussed. Finally, the effects of various parameters on the system performance are analyzed numerically.
