We consider the k‐Hyperplane Clustering problem where, given a set of m points in
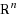, we have to partition the set into k subsets (clusters) and determine a hyperplane for each of them, so as to minimize the sum of the squares of the Euclidean distances between the points and the hyperplane of the corresponding clusters. We give a nonconvex mixed‐integer quadratically constrained quadratic programming formulation for the problem. Since even very small‐size instances are challenging for state‐of‐the‐art spatial branch‐and‐bound solvers like Couenne, we propose a heuristic in which many ‘critical’ points are reassigned at each iteration. Such points, which are likely to be ill‐assigned in the current solution, are identified using a distance‐based criterion and their number is progressively decreased to zero. Our algorithm outperforms the best available one proposed by Bradley and Mangasarian on a set of real‐world and structured randomly generated instances. For the largest instances, we obtain an average improvement in the solution quality of 54%.
