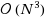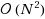A single‐period inventory placement problem for a supply system with the satisficing objective

Consider the inventory placement problem in an N‐stage supply system facing a stochastic demand for a single planning period. Each stage is a stocking point holding some form of inventory (e.g., raw materials, subassemblies, product returns or finished products) that after a suitable transformation can satisfy demand. Stocking decisions are made before demand occurs. Unsatisfied demands are lost. The revenue, salvage value, ordering, transformation, and lost sales costs are proportional. There are fixed costs for utilizing stages for stock storage. The objective is to maximize the probability of achieving a given target profit level. We prove the existence of optimal stocking decisions where at most three stages receive nonzero stocks. We also characterize properties of the optimal stocking decisions and provide an 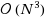$\mathcal{O}(N^3)$ algorithm for their computation. For the special case where all fixed costs are zero, the stages utilized do not depend on the demand distribution or the target level, and one can find optimal stocking decisions by performing a simple 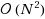$\mathcal{O}(N^2)$ search and solving a single‐variable optimization problem.