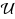New variations of the maximum coverage facility location problem

Consider a competitive facility location scenario where, given a set 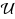$\mathcal{U}$ of n users and a set $\mathcal{F}$ of m facilities in the plane, the objective is to place a new facility in an appropriate place such that the number of users served by the new facility is maximized. Here users and facilities are considered as points in the plane, and each user takes service from its nearest facility, where the distance between a pair of points is measured in either L 1 or L 2 or L ∞ metric. This problem is also known as the maximum coverage (MaxCov) problem. In this paper, we will consider the k‐MaxCov problem, where the objective is to place k (⩾1) new facilities such that the total number of users served by these k new facilities is maximized. We begin by proposing an O(nlogn) time algorithm for the k‐MaxCov problem, when the existing facilities are all located on a single straight line and the new facilities are also restricted to lie on the same line. We then study the 2‐MaxCov problem in the plane, and propose an O(n ²) time and space algorithm in the L 1 and L ∞ metrics. In the L 2 metric, we solve the 2‐MaxCov problem in the plane in O(n ³logn) time and O(n ²logn) space. Finally, we consider the 2‐Farthest‐MaxCov problem, where a user is served by its farthest facility, and propose an algorithm that runs in O(nlogn) time, in all the three metrics.