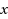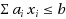| Article ID: | iaor2013733 |
| Volume: | 41 |
| Issue: | 1 |
| Start Page Number: | 74 |
| End Page Number: | 77 |
| Publication Date: | Jan 2013 |
| Journal: | Operations Research Letters |
| Authors: | Toth Paolo, Caprara Alberto, Marti Gbor, Cacchiani Valentina |
| Keywords: | programming: convex, programming: integer, scheduling, combinatorial optimization |
We provide a simple description in terms of linear inequalities of the convex hull of the nonnegative integer vectors