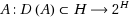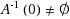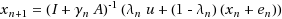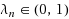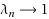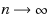| Article ID: | iaor2013657 |
| Volume: | 7 |
| Issue: | 2 |
| Start Page Number: | 415 |
| End Page Number: | 420 |
| Publication Date: | Feb 2013 |
| Journal: | Optimization Letters |
| Authors: | Boikanyo Oganeditse, Morosanu Gheorghe |
| Keywords: | proximal point algorithm, Hilbert space |
Given any maximal monotone operator