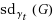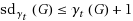The total domination subdivision number in graphs with no induced 3‐cycle and 5‐cycle

A set S of vertices of a graph G=(V,E) without isolated vertex is a total dominating set if every vertex of V(G) is adjacent to some vertex in S. The total domination number γ t (G) is the minimum cardinality of a total dominating set of G. The total domination subdivision number 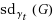${\mathrm{sd}}_{{\gamma }_t}(G)$ is the minimum number of edges that must be subdivided (each edge in G can be subdivided at most once) in order to increase the total domination number. Favaron, Karami, Khoeilar and Sheikholeslami (J. Comb. Optim. 20:76–84, 2010a) conjectured that: For any connected graph G of order n≥3, 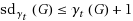${\mathrm{sd}}_{{\gamma }_t}(G)\le {\gamma }_t(G)+1$ . In this paper we use matching to prove this conjecture for graphs with no 3‐cycle and 5‐cycle. In particular this proves the conjecture for bipartite graphs.