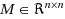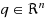| Article ID: | iaor20132056 |
| Volume: | 7 |
| Issue: | 3 |
| Start Page Number: | 519 |
| End Page Number: | 531 |
| Publication Date: | Mar 2013 |
| Journal: | Optimization Letters |
| Authors: | Hu Sheng-Long, Ni Tie |
| Keywords: | programming: quadratic |
The linear complementarity problem (LCP) is to find