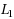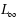Branch‐and‐bound algorithms for the partial inverse mixed integer linear programming problem

This paper presents branch‐and‐bound algorithms for the partial inverse mixed integer linear programming (PInvMILP) problem, which is to find a minimal perturbation to the objective function of a mixed integer linear program (MILP), measured by some norm, such that there exists an optimal solution to the perturbed MILP that also satisfies an additional set of linear constraints. This is a new extension to the existing inverse optimization models. Under the weighted $L_1$ and $L_{\mathrm{\infty }}$ norms, the presented algorithms are proved to finitely converge to global optimality. In the presented algorithms, linear programs with complementarity constraints (LPCCs) need to be solved repeatedly as a subroutine, which is analogous to repeatedly solving linear programs for MILPs. Therefore, the computational complexity of the PInvMILP algorithms can be expected to be much worse than that of MILP or LPCC. Computational experiments show that small‐sized test instances can be solved within a reasonable time period.