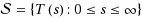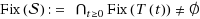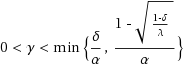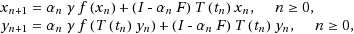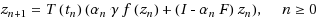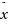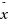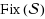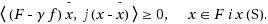Let E be a real reflexive strictly convex Banach space which has uniformly Gâteaux differentiable norm. Let
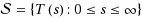 be a nonexpansive semigroup on E such that
be a nonexpansive semigroup on E such that
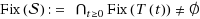 , and f is a contraction on E with coefficient 0 < α < 1. Let F be δ‐strongly accretive and λ‐strictly pseudo‐contractive with δ + λ > 1 and
, and f is a contraction on E with coefficient 0 < α < 1. Let F be δ‐strongly accretive and λ‐strictly pseudo‐contractive with δ + λ > 1 and
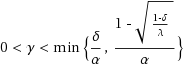 . When the sequences of real numbers {α
n
} and {t
n
} satisfy some appropriate conditions, the three iterative processes given as follows :
. When the sequences of real numbers {α
n
} and {t
n
} satisfy some appropriate conditions, the three iterative processes given as follows :
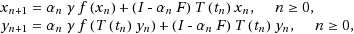 and
and
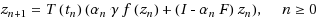 converge strongly to
converge strongly to
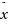 , where
, where
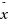 is the unique solution in
is the unique solution in
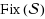 of the variational inequality
of the variational inequality
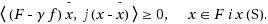 Our results extend and improve corresponding ones of Li et al. (Nonlinear Anal 70:3065–3071, 2009) and Chen and He (Appl Math Lett 20:751–757, 2007) and many others.
Our results extend and improve corresponding ones of Li et al. (Nonlinear Anal 70:3065–3071, 2009) and Chen and He (Appl Math Lett 20:751–757, 2007) and many others.