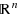| Article ID: | iaor20131199 |
| Volume: | 55 |
| Issue: | 2 |
| Start Page Number: | 261 |
| End Page Number: | 278 |
| Publication Date: | Feb 2013 |
| Journal: | Journal of Global Optimization |
| Authors: | Dearing P, Smith Andrea |
| Keywords: | heuristics, programming: convex, programming: nonlinear |
The nonlinear convex programming problem of finding the minimum covering weighted ball of a given finite set of points in