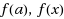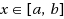| Article ID: | iaor20128597 |
| Volume: | 57 |
| Issue: | 3-4 |
| Start Page Number: | 612 |
| End Page Number: | 622 |
| Publication Date: | Feb 2013 |
| Journal: | Mathematical and Computer Modelling |
| Authors: | Dragomir S S, Momoniat E |
| Keywords: | approximation, Hilbert space |
A three point quadrature rule approximating the Riemann integral for a function of bounded variation