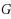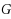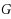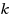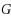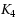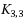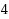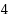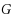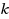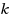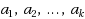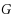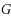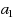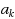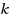A graph
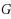 is
is
 ‐ordered if for every sequence of
‐ordered if for every sequence of
 distinct vertices of
distinct vertices of
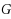 , there exists a cycle in
, there exists a cycle in
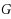 containing these
containing these
 vertices in the specified order. It is
vertices in the specified order. It is
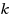 ‐ordered‐Hamiltonian if, in addition, the required cycle is a Hamiltonian cycle in
‐ordered‐Hamiltonian if, in addition, the required cycle is a Hamiltonian cycle in
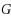 . The question of the existence of an infinite class of 3‐regular 4‐ordered‐Hamiltonian graphs was posed in Ng and Schultz in 1997 [2]. At the time, the only known examples of such graphs were
. The question of the existence of an infinite class of 3‐regular 4‐ordered‐Hamiltonian graphs was posed in Ng and Schultz in 1997 [2]. At the time, the only known examples of such graphs were
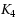 and
and
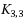 . Some progress was made by Mészáros in 2008 [21] when the Petersen graph was found to be 4‐ordered and the Heawood graph was proved to be 4‐ordered‐Hamiltonian; moreover, an infinite class of 3‐regular 4‐ordered graphs was found. In 2010, a subclass of the generalized Petersen graphs was shown to be 4‐ordered in Hsu et al. [9], with an infinite subset of this subclass being 4‐ordered‐Hamiltonian, thus answering the open question. However, these graphs are bipartite. In this paper we extend the result to another subclass of the generalized Petersen graphs. In particular, we find the first class of infinite non‐bipartite graphs that are both
. Some progress was made by Mészáros in 2008 [21] when the Petersen graph was found to be 4‐ordered and the Heawood graph was proved to be 4‐ordered‐Hamiltonian; moreover, an infinite class of 3‐regular 4‐ordered graphs was found. In 2010, a subclass of the generalized Petersen graphs was shown to be 4‐ordered in Hsu et al. [9], with an infinite subset of this subclass being 4‐ordered‐Hamiltonian, thus answering the open question. However, these graphs are bipartite. In this paper we extend the result to another subclass of the generalized Petersen graphs. In particular, we find the first class of infinite non‐bipartite graphs that are both
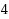 ‐ordered‐Hamiltonian and
‐ordered‐Hamiltonian and
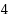 ‐ordered‐Hamiltonian‐connected, which can be seen as a solution to an extension of the question posted in Ng and Schultz in 1997 [2]. (A graph
‐ordered‐Hamiltonian‐connected, which can be seen as a solution to an extension of the question posted in Ng and Schultz in 1997 [2]. (A graph
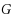 is
is
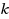 ‐ordered‐Hamiltonian‐connected if for every sequence of
‐ordered‐Hamiltonian‐connected if for every sequence of
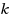 distinct vertices
distinct vertices
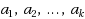 of
of
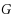 , there exists a Hamiltonian path in
, there exists a Hamiltonian path in
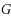 from
from
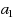 to
to
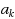 where these
where these
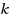 vertices appear in the specified order.)
vertices appear in the specified order.)