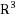| Article ID: | iaor20128567 |
| Volume: | 57 |
| Issue: | 3-4 |
| Start Page Number: | 425 |
| End Page Number: | 434 |
| Publication Date: | Feb 2013 |
| Journal: | Mathematical and Computer Modelling |
| Authors: | Morais J |
| Keywords: | graphs |
The object of this paper is to construct a complete orthogonal system of monogenic polynomials as solutions of the Moisil–Théodoresco system over prolate spheroids in