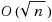| Article ID: | iaor20127628 |
| Volume: | 33 |
| Issue: | 4 |
| Start Page Number: | 421 |
| End Page Number: | 437 |
| Publication Date: | Oct 1999 |
| Journal: | RAIRO - Operations Research |
| Authors: | Milis I, Bampis E, Manoussakis Y |
| Keywords: | optimization, heuristics |
Given a graph with colored edges, a Hamiltonian cycle is called alternating if its successive edges differ in color. The problem of finding such a cycle, even for 2‐edge‐colored graphs, is trivially NP‐complete, while it is known to be polynomial for 2‐edge‐colored complete graphs. In this paper we study the parallel complexity of finding such a cycle, if any, in 2‐edge‐colored complete graphs. We give a new characterization for such a graph admitting an alternating Hamiltonian cycle which allows us to derive a parallel algorithm for the problem. Our parallel solution uses a perfect matching algorithm putting the alternating Hamiltonian cycle problem to the RNC class. In addition, a sequential version of our parallel algorithm improves the computation time of the fastest known sequential algorithm for the alternating Hamiltonian cycle problem by a factor of