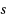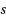A generalization of the Wiener rational basis functions on infinite intervals, Part II – Numerical investigation

In Part I we introduced the generalized Wiener rational basis functions, and here in Part II we continue our investigation with numerical experiments. Wiener’s generalized basis can utilize the fast Fourier transform for integer values of the decay parameter 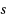$s$ ; we outline two algorithms for doing so. In addition, the issue of Galerkin representations for polynomial nonlinearities of expansions is addressed. The Wiener basis set is compared against domain truncation methods (Fourier and Chebyshev polynomials), Hermite functions, Sinc interpolations, and mapped Chebyshev expansions, and we show that for both exponentially and algebraically decaying functions, the Wiener approximation is as good as or superior to these alternatives. In addition, we carry out preliminary investigations regarding tuning of the decay parameter 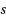$s$ . Numerical simulations of Korteweg–de Vries type equations show the effectiveness of the Wiener expansion. We also explore the practical use of the Wiener basis functions on the semi‐infinite interval, which is compared against Laguerre function methods and other Jacobi polynomial mappings.