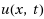| Article ID: | iaor20125473 |
| Volume: | 237 |
| Issue: | 1 |
| Start Page Number: | 432 |
| End Page Number: | 441 |
| Publication Date: | Jan 2013 |
| Journal: | Journal of Computational and Applied Mathematics |
| Authors: | Le Triet Minh, Pham Quan Hoang, Dang Trong Duc, Nguyen Tuan Huy |
| Keywords: | estimation |
We consider the problem of determining the temperature