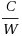Semidefinite Programming Based Algorithms for the Sparsest Cut Problem

In this paper we analyze a known relaxation for the Sparsest Cut problem based on positive semidefinite constraints, and we present a branch and bound algorithm and heuristics based on this relaxation. The relaxed formulation and the algorithms were tested on small and moderate sized instances. It leads to values very close to the optimum solution values. The exact algorithm could obtain solutions for small and moderate sized instances, and the best heuristics obtained optimum or near optimum solutions for all tested instances. The semidefinite relaxation gives a lower bound $\frac{C}{W}$ and each heuristic produces a cut S with a ratio $\frac{c_S}{w_S}$ , where either c S is at most a factor of C or w S is at least a factor of W. We solved the semidefinite relaxation using a semi‐infinite cut generation with a commercial linear programming package adapted to the sparsest cut problem. We showed that the proposed strategy leads to a better performance compared to the use of a known semidefinite programming solver.