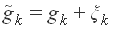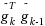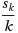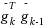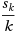New stochastic approximation algorithms with adaptive step sizes

This paper considers the stochastic approximation problem in which the gradient of the function is disturbed by noise. In other words, at each point x k , instead of the exact gradient g k , only noisy measurement ${\sim }_k=g_k+{\xi }_k$ is available, where ξ k denotes the noise. To accelerate the classical Robbins–Monro algorithm, Kesten (Ann Math Stat 29:41–59, 1958) and Delyon and Juditsky (SIAM J Optim 3:868–881, 1993) considered the use of the quantity s k that stands for the number of changes of the sign of ${\tilde{g}}_k^T{\tilde{g}}_{k-1}$ . Assuming the presence of state independent noise, we discuss in this paper the properties of the quantity $\frac{s_k}{k}$ that stands for the change frequency of the sign of ${\tilde{g}}_k^T{\tilde{g}}_{k-1}$ and design new stochastic approximation algorithms based on the quantity $\frac{s_k}{k}$ . The almost sure convergence of the new algorithms are also established. The numerical results show that the algorithms are promising.