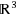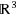The discretizable distance geometry problem

We introduce the discretizable distance geometry problem in 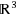${ℝ}^3$ (DDGP3), which consists in a subclass of instances of the Distance Geometry Problem for which an embedding in 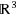${ℝ}^3$ can be found by means of a discrete search. We show that the DDGP3 is a generalization of the discretizable molecular distance geometry problem (DMDGP), and we discuss the main differences between the two problems. We prove that the DDGP3 is NP‐hard and we extend the Branch & Prune (BP) algorithm, previously used for the DMDGP, for solving instances of the DDGP3. Protein graphs may or may not be in DMDGP and/or DDGP3 depending on vertex orders and edge density. We show experimentally that as distance thresholds decrease, PDB protein graphs which fail to be in the DMDGP still belong to DDGP3, which means that they can still be solved using a discrete search.