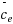The Fixed‐Charge Shortest‐Path Problem

Consider a network 𝒩 =(N, A) and associate with each arc e ∈ A a fixed cost ce for using arc e, an interval [le , ue ] (le , ue ∈ ℤ) specifying the range of allowable resource consumption quantities along arc e, and a per‐unit cost 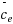${\overline{c}}_e$ for resource consumed along e. Furthermore, for each node n ∈ N, let Un ∈ ℤ be the maximum amount of resource consumption a path can accumulate before visiting node n. Given a source node ns ∈ N and sink node nt ∈ N, the fixed‐charge shortest‐path problem (FCSPP) seeks to find a minimum‐cost‐feasible path from ns to nt . When resource consumption is simply additive, the resource‐constrained shortest‐path problem (RCSPP) is a special case of FCSPP. We develop a new dynamic programming algorithm for FCSPP. The algorithm uses solutions from labeling and dominance techniques for standard RCSPPs on slightly modified problems, and it combines these solutions by exploiting the structure provided by certain classes of knapsack problems to efficiently construct an optimal solution to FCSPP. Computational experiments demonstrate that our algorithm is often several orders of magnitude faster than naive dynamic programming procedures.