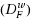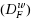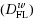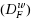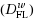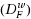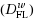Weak Fenchel and weak Fenchel‐Lagrange conjugate duality for nonconvex scalar optimization problems

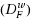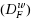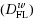In this work, by using weak conjugate maps given in (Azimov and Gasimov,1999), weak Fenchel conjugate dual problem, $(D_F^w)$ , and weak Fenchel Lagrange conjugate dual problem $(D_{\mathrm{FL}}^w)$ are constructed. Necessary and sufficient conditions for strong duality for the $(D_F^w)$ , $(D_{\mathrm{FL}}^w)$ and primal problem are given. Furthermore, relations among the optimal objective values of dual problem constructed by using Augmented Lagrangian in (Azimov and Gasimov, in Int J Appl Math 1:171–192, 1999), 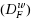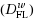$(D_F^w)$ , $(D_{\mathrm{FL}}^w)$ dual problems and primal problem are examined. 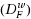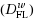Lastly, necessary and sufficient optimality conditions for the primal and the dual problems $(D_F^w)$ and $(D_{\mathrm{FL}}^w)$ are established.