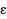Decomposition strategy for the stochastic pooling problem

The stochastic pooling problem is a type of stochastic mixed‐integer bilinear program arising in the integrated design and operation of various important industrial networks, such as gasoline blending, natural gas production and transportation, water treatment, etc. This paper presents a rigorous decomposition method for the stochastic pooling problem, which guarantees finding an 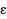$ϵ$ ‐optimal solution with a finite number of iterations. By convexification of the bilinear terms, the stochastic pooling problem is relaxed into a lower bounding problem that is a potentially large‐scale mixed‐integer linear program (MILP). Solution of this lower bounding problem is then decomposed into a sequence of relaxed master problems, which are MILPs with much smaller sizes, and primal bounding problems, which are linear programs. The solutions of the relaxed master problems yield a sequence of nondecreasing lower bounds on the optimal objective value, and they also generate a sequence of integer realizations defining the primal problems which yield a sequence of nonincreasing upper bounds on the optimal objective value. The decomposition algorithm terminates finitely when the lower and upper bounds coincide (or are close enough), or infeasibility of the problem is indicated. Case studies involving two example problems and two industrial problems demonstrate the dramatic computational advantage of the proposed decomposition method over both a state‐of‐the‐art branch‐and‐reduce global optimization method and explicit enumeration of integer realizations, particularly for large‐scale problems.