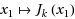We propose a heuristic for 0/1 programs based on the recent ‘joint + marginal’ approach of the first author for parametric polynomial optimization. The idea is to first consider the n‐variable (x
1,… , x
n
) problem as a (n−1)‐variable problem (x
2,… , x
n
) with the variable x
1 being now a parameter taking value in {0, 1}. One then solves a hierarchy of what we call ‘joint + marginal’ semidefinite relaxations whose duals provide a sequence of polynomial approximations
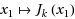 that converges to the optimal value function J (x
1) (as a function of the parameter x
1). One considers a fixed index k in the hierarchy and if J
k
(1) > J
k
(0) then one decides x
1 = 1 and x
1 = 0 otherwise. The quality of the approximation depends on how large k can be chosen (in general, for significant size problems, k = 1 is the only choice). One iterates the procedure with now a (n−2)‐variable problem with one parameter
that converges to the optimal value function J (x
1) (as a function of the parameter x
1). One considers a fixed index k in the hierarchy and if J
k
(1) > J
k
(0) then one decides x
1 = 1 and x
1 = 0 otherwise. The quality of the approximation depends on how large k can be chosen (in general, for significant size problems, k = 1 is the only choice). One iterates the procedure with now a (n−2)‐variable problem with one parameter
 , etc. Variants are also briefly described as well as some preliminary numerical experiments on the MAXCUT, k‐cluster and 0/1 knapsack problems.
, etc. Variants are also briefly described as well as some preliminary numerical experiments on the MAXCUT, k‐cluster and 0/1 knapsack problems.