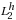Convergence Analysis of Weighted Difference Approximations on Piecewise Uniform Grids to a Class of Singularly Perturbed Functional Differential Equations

We consider the numerical approximation of a singularly perturbed time delayed convection diffusion problem on a rectangular domain. Assuming that the coefficients of the differential equation be smooth, we construct and analyze a higher order accurate finite difference method that converges uniformly with respect to the singular perturbation parameter. The method presented is a combination of the central difference spatial discretization on a Shishkin mesh and a weighted difference time discretization on a uniform mesh. A priori explicit bounds on the solution of the problem are established. These bounds on the solution and its derivatives are obtained using a suitable decomposition of the solution into regular and layer components. It is shown that the proposed method is $L_2^h$ ‐stable. The analysis done permits its extension to the case of adaptive meshes which may be used to improve the solution. Numerical examples are presented to demonstrate the effectiveness of the method. The convergence obtained in practical satisfies the theoretical predictions.