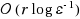Polynomial Convergence of Second‐Order Mehrotra‐Type Predictor‐Corrector Algorithms over Symmetric Cones

This paper presents an extension of the variant of Mehrotra’s predictor–corrector algorithm which was proposed by Salahi and Mahdavi‐Amiri (Appl. Math. Comput. 183:646–658, 2006) for linear programming to symmetric cones. This algorithm incorporates a safeguard in Mehrotra’s original predictor–corrector algorithm, which keeps the iterates in the prescribed neighborhood and allows us to get a reasonably large step size. In our algorithm, the safeguard strategy is not necessarily used when the affine scaling step behaves poorly, which is different from the algorithm of Salahi and Mahdavi‐Amiri. We slightly modify the maximum step size in the affine scaling step and extend the algorithm to symmetric cones using the machinery of Euclidean Jordan algebras. Based on the Nesterov–Todd direction, we show that the iteration‐complexity bound of the proposed algorithm is $𝒪(r\log {ϵ}^{-1})$ , where r is the rank of the associated Euclidean Jordan algebras and ϵ>0 is the required precision.