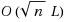| Article ID: | iaor20123816 |
| Volume: | 75 |
| Issue: | 2 |
| Start Page Number: | 165 |
| End Page Number: | 183 |
| Publication Date: | Apr 2012 |
| Journal: | Mathematical Methods of Operations Research |
| Authors: | Liu Hongwei, Liu Changhe |
| Keywords: | interior point methods, programming (semidefinite) |
In this paper, we propose a second‐order corrector interior‐point algorithm for semidefinite programming (SDP). This algorithm is based on the wide neighborhood. The complexity bound is