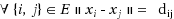| Article ID: | iaor20123497 |
| Volume: | 6 |
| Issue: | 4 |
| Start Page Number: | 783 |
| End Page Number: | 796 |
| Publication Date: | Apr 2012 |
| Journal: | Optimization Letters |
| Authors: | Lee Jon, Sviridenko Maxim, Liberti Leo, Lavor Carlile, Mucherino Antonio, Lee-St. John Audrey |
| Keywords: | sets, decision |
Given a weighted, undirected simple graph