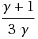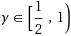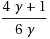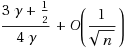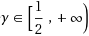On the maximum TSP with γ‐parameterized triangle inequality

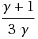The maximum TSP with γ‐parameterized triangle inequality is defined as follows. Given a complete graph G = (V, E, w) in which the edge weights satisfy w(uv) ≤ γ (w(ux) + w(xv)) for all distinct nodes $u,x,v\in V$ , find a tour with maximum weight that visits each node exactly once. Recently, Zhang et al. (Theor Comput Sci 411(26–28):2537–2541, 2010) proposed a $\frac{\gamma +1}{3\gamma }$ ‐approximation algorithm for 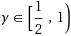$\gamma \in \left[\frac{1}{2}\text{,}1\right)$ . In this paper, we show that the approximation ratio of Kostochka and Serdyukov’s algorithm (Upravlyaemye Sistemy 26:55–59, 1985) is 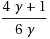$\frac{4\gamma +1}{6\gamma }$ , and the expected approximation ratio of Hassin and Rubinstein’s randomized algorithm (Inf Process Lett 81(5):247–251, 2002) is $\frac{3\gamma +\frac{1}{2}}{4\gamma }+O\left(\frac{1}{\sqrt{n}}\right)$ , for $\gamma \in [\frac{1}{2}\text{,}+\mathrm{\infty })$ . These improve the result in Zhang et al. (Theor Comput Sci 411(26–28):2537–2541, 2010) and generalize the results in Hassin and Rubinstein and Kostochka and Serdyukov (Inf Process Lett 81(5):247–251, 2002; Upravlyaemye Sistemy 26:55–59, 1985).