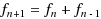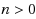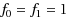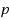| Article ID: | iaor20122346 |
| Volume: | 59 |
| Issue: | 1 |
| Start Page Number: | 233 |
| End Page Number: | 246 |
| Publication Date: | Jan 2010 |
| Journal: | Computers and Mathematics with Applications |
| Authors: | Cureg Edgardo, Mukherjea Arunava |
| Keywords: | Lyapunov |
Random Fibonacci sequences are stochastic versions of the classical Fibonacci sequence