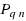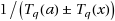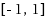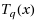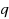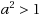| Article ID: | iaor20122331 |
| Volume: | 59 |
| Issue: | 1 |
| Start Page Number: | 382 |
| End Page Number: | 390 |
| Publication Date: | Jan 2010 |
| Journal: | Computers and Mathematics with Applications |
| Authors: | Dehghan Mehdi, Eslahchi M R |
| Keywords: | approximation, Chebyshev |
In this research paper using the Chebyshev expansion, we explicitly determine the best uniform polynomial approximation out of