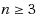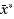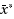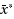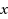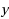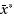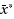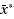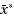A Weiszfeld algorithm for the solution of an asymmetric extension of the generalized Fermat location problem

The Generalized Fermat Problem (in the plane) is: given 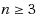$n\ge 3$ destination points find the point 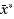${\overline{x}}^{*}$ which minimizes the sum of Euclidean distances from 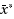${\overline{x}}^{*}$ to each of the destination points.The Weiszfeld iterative algorithm for this problem is globally convergent, independent of the initial guess. Also, a test is available, à priori, to determine when 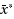${\overline{x}}^{*}$ a destination point. This paper generalizes earlier work by the first author by introducing an asymmetric Euclidean distance in which, at each destination, the 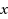$x$ ‐component is weighted differently from the 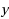$y$ ‐component. A Weiszfeld algorithm is studied to compute 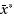${\overline{x}}^{*}$ and is shown to be a descent method which is globally convergent (except possibly for a denumerable number of starting points). Local convergence properties are characterized. When 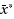${\overline{x}}^{*}$ is not a destination point the iteration matrix at ${\overline{x}}^{*}$ is shown to be convergent and local convergence is always linear. 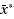When ${\overline{x}}^{*}$ is a destination point, local convergence can be linear, sub‐linear or super‐linear, depending upon a computable criterion. A test, which does not require iteration, for 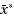${\overline{x}}^{*}$ to be a destination, is derived. Comparisons are made between the symmetric and asymmetric problems. Numerical examples are given.