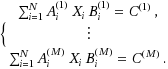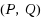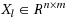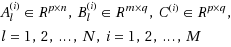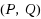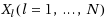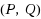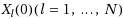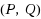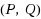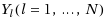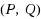A finite iterative algorithm for solving the generalized (P,Q) ‐reflexive solution of the linear systems of matrix equations

In this paper, we proposed an algorithm for solving the linear systems of matrix equations 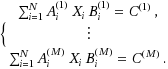$\{\begin{array}{c}{\sum }_{i=1}^N{A}_i^{\left(1\right)}{X}_i{B}_i^{\left(1\right)}=C^{\left(1\right)}\text{,}\hfill \\ ⋮\hfill \\ {\sum }_{i=1}^N{A}_i^{\left(M\right)}{X}_i{B}_i^{\left(M\right)}=C^{\left(M\right)}\text{.}\hfill \end{array}$ over the generalized 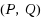$(P,Q)$ ‐reflexive matrix 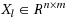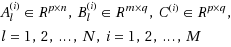$X_l\in R^{n\times m}$ ( $A_l^{\left(i\right)}\in R^{p\times n},B_l^{\left(i\right)}\in R^{m\times q},C^{\left(i\right)}\in R^{p\times q},l=1,2,\dots ,N,i=1,2,\dots ,M$ ). According to the algorithm, the solvability of the problem can be determined automatically. When the problem is consistent over the generalized 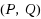$(P,Q)$ ‐reflexive matrix 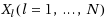$X_l(l=1,\dots ,N)$ , for any generalized 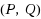$(P,Q)$ ‐reflexive initial iterative matrices 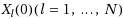$X_l\left(0\right)(l=1,\dots ,N)$ , the generalized 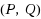$(P,Q)$ ‐reflexive solution can be obtained within finite iterative steps in the absence of roundoff errors. The unique least‐norm generalized 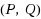$(P,Q)$ ‐reflexive solution can also be derived when the appropriate initial iterative matrices are chosen. A sufficient and necessary condition for which the linear systems of matrix equations is inconsistent is given. Furthermore, the optimal approximate solution for a group of given matrices 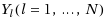$Y_l(l=1,\dots ,N)$ can be derived by finding the least‐norm generalized 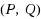$(P,Q)$ ‐reflexive solution of a new corresponding linear system of matrix equations. Finally, we present a numerical example to verify the theoretical results of this paper.