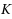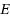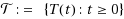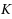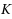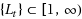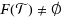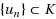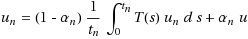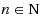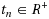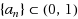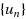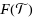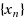Let
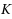 be a nonempty closed convex subset of a real Banach space
be a nonempty closed convex subset of a real Banach space
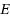 . Let
. Let
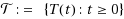 be a strongly continuous semigroup of asymptotically nonexpansive mappings from
be a strongly continuous semigroup of asymptotically nonexpansive mappings from
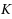 into
into
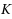 with a sequence
with a sequence
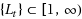 . Suppose
. Suppose
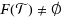 . Then, for a given
. Then, for a given
 there exists a sequence
there exists a sequence
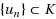 such that
such that
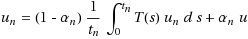 , for
, for
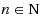 , where
, where
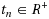 ,
,
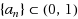 and
and
 satisfy certain conditions. Suppose, in addition, that
satisfy certain conditions. Suppose, in addition, that
 is reflexive strictly convex with a Gâteaux differentiable norm. Then, the sequence
is reflexive strictly convex with a Gâteaux differentiable norm. Then, the sequence
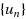 converges strongly to a point of
converges strongly to a point of
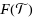 . Furthermore, an explicit sequence
. Furthermore, an explicit sequence
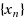 which converges strongly to a fixed point of
which converges strongly to a fixed point of
 is proved.
is proved.