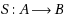Discrete optimization in partially ordered sets

The primary aim of this article is to resolve a global optimization problem in the setting of a partially ordered set that is equipped with a metric. Indeed, given non‐empty subsets A and B of a partially ordered set that is endowed with a metric, and a non‐self mapping $S:A⟶B$ , this paper discusses the existence of an optimal approximate solution, designated as a best proximity point of the mapping S, to the equation Sx = x, where S is a proximally increasing, ordered proximal contraction. An algorithm for determining such an optimal approximate solution is furnished. Further, the result established in this paper realizes an interesting fixed point theorem in the setting of partially ordered set as a special case.