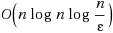New parameterized kernel functions for linear optimization

Recent studies on the kernel function‐based primal‐dual interior‐point algorithms indicate that a kernel function not only represents a measure of the distance between the iteration and the central path, but also plays a critical role in improving the computational complexity of an interior‐point algorithm. In this paper, we propose a new class of parameterized kernel functions for the development of primal‐dual interior‐point algorithms for solving linear programming problems. The properties of the proposed kernel functions and corresponding parameters are investigated. The results lead to a complexity bounds of $O\left(n\log n\log \frac{n}{ϵ}\right)$ for the large‐update primal‐dual interior point methods. To the best of our knowledge, this is the best known bound achieved.