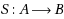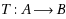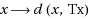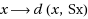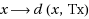Common best proximity points: global minimization of multi‐objective functions

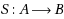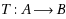Given non‐empty subsets A and B of a metric space, let $S:A⟶B$ and $T:A⟶B$ be non‐self mappings. Due to the fact that S and T are non‐self mappings, the equations Sx = x and Tx = x are likely to have no common solution, known as a common fixed point of the mappings S and T. Consequently, when there is no common solution, it is speculated to determine an element x that is in close proximity to Sx and Tx in the sense that d(x, Sx) and d(x, Tx) are minimum. As a matter of fact, common best proximity point theorems inspect the existence of such optimal approximate solutions, called common best proximity points, to the equations Sx = x and Tx = x in the case that there is no common solution. 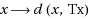It is highlighted that the real valued functions $x⟶d(x,\mathrm{Sx})$ and $x⟶d(x,\mathrm{Tx})$ assess the degree of the error involved for any common approximate solution of the equations Sx = x and Tx = x. 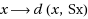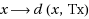Considering the fact that, given any element x in A, the distance between x and Sx, and the distance between x and Tx are at least d(A, B), a common best proximity point theorem affirms global minimum of both functions $x⟶d(x,\mathrm{Sx})$ and $x⟶d(x,\mathrm{Tx})$ by imposing a common approximate solution of the equations Sx = x and Tx = x to satisfy the constraint that d(x, Sx) = d(x, Tx) = d(A, B). The purpose of this article is to derive a common best proximity point theorem for proximally commuting non‐self mappings, thereby producing common optimal approximate solutions of certain simultaneous fixed point equations in the event there is no common solution.