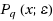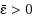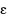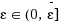An approach to constrained global optimization based on exact penalty functions

In the field of global optimization many efforts have been devoted to solve unconstrained global optimization problems. The aim of this paper is to show that unconstrained global optimization methods can be used also for solving constrained optimization problems, by resorting to an exact penalty approach. In particular, we make use of a non‐differentiable exact penalty function $P_q(x;ϵ)$ . We show that, under weak assumptions, there exists a threshold value $\overline{ϵ}>0$ of the penalty parameter $ϵ$ such that, for any $ϵ\in (0,\overline{ϵ}]$ , any global minimizer of P q is a global solution of the related constrained problem and conversely. On these bases, we describe an algorithm that, by combining an unconstrained global minimization technique for minimizing P q for given values of the penalty parameter $ϵ$ and an automatic updating of $ϵ$ that occurs only a finite number of times, produces a sequence {x ^k } such that any limit point of the sequence is a global solution of the related constrained problem. In the algorithm any efficient unconstrained global minimization technique can be used. In particular, we adopt an improved version of the DIRECT algorithm. Some numerical experimentation confirms the effectiveness of the approach.