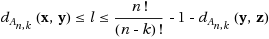The paths embedding of the arrangement graphs with prescribed vertices in given position

Let n and k be positive integers with n−k≥2. The arrangement graph A n,k is recognized as an attractive interconnection networks. Let x, y, and z be three different vertices of A n,k . Let l be any integer with 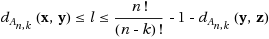$d_{A_{n,k}}(x,y)\le l\le \frac{n!}{(n‐k)!}‐1‐d_{A_{n,k}}(y,z)$ . We shall prove the following existance properties of Hamiltonian path: (1) for n−k≥3 or (n,k)=(3,1), there exists a Hamiltonian path R(x,y,z;l) from x to z such that d R(x,y,z;l)(x,y)=l; (2) for n−k=2 and n≥5, there exists a Hamiltonian path R(x,y,z;l) except for the case that x, y, and z are adjacent to each other.