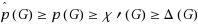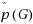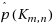Parity and strong parity edge‐colorings of graphs

A parity walk in an edge‐coloring of a graph is a walk along which each color is used an even number of times. A parity edge‐coloring (respectively, strong parity edge‐coloring) is an edge‐coloring in which there is no nontrivial parity path (respectively, open parity walk). The parity edge‐chromatic number p(G) (respectively, strong parity edge‐chromatic number $\hat{p}(G)$ ) is the least number of colors in a parity edge‐coloring (respectively, strong parity edge‐coloring) of G. 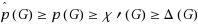Notice that $\hat{p}(G)\ge p(G)\ge \chi \prime (G)\ge \Delta (G)$ for any graph G. In this paper, we determine 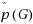$\hat{p}(G)$ and p(G) for some complete bipartite graphs and some products of graphs. For instance, we determine 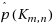$\hat{p}(K_{m,n})$ and p(K m,n ) for m≤n with n≡0,−1,−2 (mod 2^{⌈lg m⌉}).