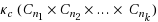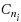On cyclic vertex‐connectivity of Cartesian product digraphs

For a strongly connected digraph D=(V(D),A(D)), a vertex‐cut S⊆V(D) is a cyclic vertex‐cut of D if D−S has at least two strong components containing directed cycles. The cyclic vertex‐connectivity κ c (D) is the minimum cardinality of all cyclic vertex‐cuts of D. In this paper, we study κ c (D) for Cartesian product digraph D=D 1×D 2, where D 1,D 2 are two strongly connected digraphs. We give an upper bound and a lower bound for κ c (D). Furthermore, the exact value of 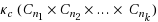${\kappa }_c(C_{n_1}\times C_{n_2}\times \dots \times C_{n_k})$ is determined, where 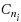$C_{n_i}$ is the directed cycle of length n i for i=1,2,…,k.