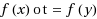A variation of the classical channel assignment problem is to assign a radio channel which is a nonnegative integer to each radio transmitter so that ‘close’ transmitters must receive different channels and ‘very close’ transmitters must receive channels that are at least two channels apart. The goal is to minimize the span of a feasible assignment. This channel assignment problem can be modeled with distance‐dependent graph labelings. A k‐L(2,1)‐labeling of a graph G is a mapping f from the vertex set of G to the set {0,1,2,…,k} such that |f(x)−f(y)|≥2 if d(x,y)=1 and
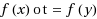if d(x,y)=2, where d(x,y) is the distance between vertices x and y in G. The minimum k for which G admits an k‐L(2,1)‐labeling, denoted by λ(G), is called the λ‐number of G. Very little is known about λ‐numbers of 3‐regular graphs. In this paper we focus on an important subclass of 3‐regular graphs called generalized Petersen graphs. For an integer n≥3, a graph G is called a generalized Petersen graph of order n if and only if G is a 3‐regular graph consisting of two disjoint cycles (called inner and outer cycles) of length n, where each vertex of the outer (resp. inner) cycle is adjacent to exactly one vertex of the inner (resp. outer) cycle. In 2002, Georges and Mauro conjectured that λ(G)≤7 for all generalized Petersen graphs G of order n≥7. Later, Adams, Cass and Troxell proved that Georges and Mauro’s conjecture is true for orders 7 and 8. In this paper it is shown that Georges and Mauro’s conjecture is true for generalized Petersen graphs of orders 9, 10, 11 and 12.
