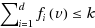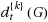The total {k}‐domatic number of wheels and complete graphs

Let k be a positive integer and let G be a graph with vertex set V(G). The total {k}‐dominating function (T{k}DF) of a graph G is a function f from V(G) to the set {0,1,2,…,k}, such that for each vertex v∈V(G), the sum of the values of all its neighbors assigned by f is at least k. A set {f 1,f 2,…,f d } of pairwise different T{k}DFs of G with the property that 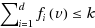${\sum }_{i=1}^d{f}_i(v)\le k$ for each v∈V(G), is called a total {k}‐dominating family (T{k}D family) of G. The total {k}‐domatic number of a graph G, denoted by 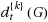$d_t^{\{k\}}(G)$ , is the maximum number of functions in a T{k}D family. In this paper, we determine the exact values of the total {k}‐domatic numbers of wheels and complete graphs, which answers an open problem of Sheikholeslami and Volkmann (J. Comb. Optim., 2010) and completes a result in the same paper.