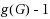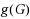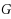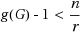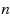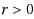| Article ID: | iaor20125786 |
| Volume: | 9 |
| Issue: | 4 |
| Start Page Number: | 236 |
| End Page Number: | 240 |
| Publication Date: | Nov 2012 |
| Journal: | Discrete Optimization |
| Authors: | Hertz Alain, Gendron Bernard, St-Louis Patrick |
| Keywords: | graphs |
A total dominating set in a digraph