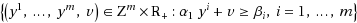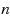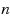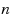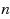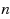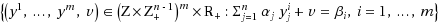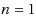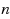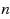Mixed n‐step MIR inequalities: Facets for the n‐mixing set

Günlük and Pochet [O. Günlük, Y. Pochet, Mixing mixed integer inequalities. Mathematical Programming 90 (2001) 429–457] proposed a procedure to mix mixed integer rounding (MIR) inequalities. The mixed MIR inequalities define the convex hull of the mixing set 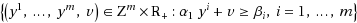$\{(y^1,\dots ,y^m,v)\in {‐{Z}}^m\times {‐{R}}_{+}:{\alpha }_1{y}^i+v\ge {\beta }_i,i=1,\dots ,m\}$ and can also be used to generate valid inequalities for general as well as several special mixed integer programs (MIPs). In another direction, Kianfar and Fathi [K. Kianfar, Y. Fathi, Generalized mixed integer rounding inequalities: facets for infinite group polyhedra. Mathematical Programming 120 (2009) 313–346] introduced the 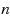$n$ ‐step MIR inequalities for the mixed integer knapsack set through a generalization of MIR. In this paper, we generalize the mixing procedure to the 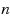$n$ ‐step MIR inequalities and introduce the mixed 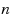$n$ ‐step MIR inequalities. We prove that these inequalities define facets for a generalization of the mixing set with 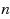$n$ integer variables in each row (which we refer to as the 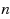$n$ ‐mixing set), i.e. 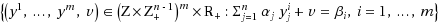$\{(y^1,\dots ,y^m,v)\in {(‐{Z}\times {‐{Z}}_{+}^{n‐1})}^m\times {‐{R}}_{+}:{?}_{j=1}^n{a}_j{y}_j^i+v={\beta }_i,i=1,\dots ,m\}$ . The mixed MIR inequalities are simply the special case of 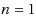$n=1$ . We also show that mixed $n$ ‐step MIR can generate valid inequalities based on multiple constraints for general MIPs. 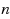Moreover, we introduce generalizations of the capacitated lot‐sizing and facility location problems, which we refer to as the multi‐module problems, and show that mixed $n$ ‐step MIR can be used to generate valid inequalities for these generalizations. Our computational results on small MIPLIB instances as well as a set of multi‐module lot‐sizing instances justify the effectiveness of the mixed 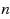$n$ ‐step MIR inequalities.