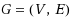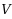Memetic search for the max‐bisection problem

Given an undirected graph 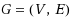$G=(V,E)$ with weights on the edges, the max‐bisection problem (MBP) is to find a partition of the vertex set 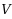$V$ into two subsets V 1 and V 2 of equal cardinality such that the sum of the weights of the edges crossing V 1 and V 2 is maximized. Relaxing the equal cardinality, constraint leads to the max‐cut problem (MCP). In this work, we present a memetic algorithm for MBP which integrates a grouping crossover operator and a tabu search optimization procedure. The proposed crossover operator preserves the largest common vertex groupings with respect to the parent solutions while controlling the distance between the offspring solution and its parents. Extensive experimental studies on 71 well‐known G‐set benchmark instances demonstrate that our memetic algorithm improves, in many cases, the current best known solutions for both MBP and MCP.