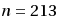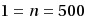Arranging a fixed number n of equal non‐overlapping circles in a rectangle with variable aspect ratio is a non‐standard packing problem. It arises if one has to decide how a certain number of circular items should be packed into a rectangular box when no assumption is made on the shape of the box. How must the box be designed to achieve the maximum packing density? This special problem was investigated by Lubachevsky and Graham in 2003, where they classified record packings for
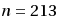. However, their work lacks a precise treatment of the closure of observed vacancies as well as any numerical data of the best arrangements found. This article introduces a shorter notation for hexagonal dense packings in rectangular containers. Furthermore, it describes a deterministic procedure for the optimization of packings that differ from usual regular hexagonal patterns by one or more vacancies, without relying on simulation programs. A couple of improvements were found (for n=37, 101, 146, 169) and numerical values are given for all packings in the extended range
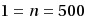(except for n=393, 411, 421, 453). Numerical results are also available at http://www.packomania.com/crc_var/
